Powers

When we multiply a number by itself, we usually use a more concise notation. For example:

3 = 3\(^1\)	(read as '3' or '3 to the power 1')
3 × 3 = 3\(^2\)	(read as '3 squared')
3 × 3 × 3 = 3\(^3\)	(read as '3 cubed')
3 × 3 × 3 × 3 = 3\(^4\)	(read as '3 to the power 4' or as '3 to the 4th')
3 × 3 × 3 × 3 × 3 = 3\(^5\)	(read as '3 to the power 5' or as '3 to the 5')
3 × 3 × 3 × 3 × 3 × 3 = 3\(^6\)	(read as '3 to the power 6' or as '3 to the 6')

The expression 3\(^5\) is called a power of 5.

The raised 5 in 3\(^5\) is called the index of the power.

The number 3 in 3\(^5\) is called the base of the power.

Geometrical representation of powers

The terms '3 squared' for \(3^2\) and '3 cubed' for \(3^3\) come from geometry. You might have seen before we can arrange \(3^2\) dots in a square and \(3^3\) dots in a cube:

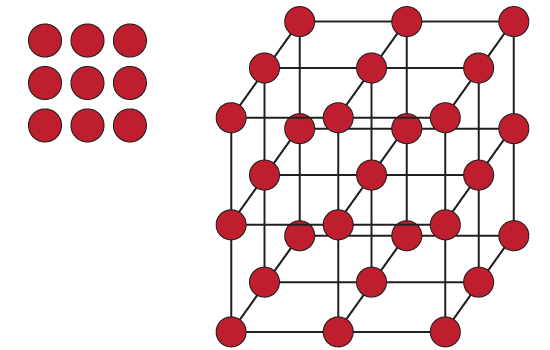
The numbers \(0^2 = 0, 1^2 = 1, 2^2 = 4, 3^2 = 9\)… are called squares.

The numbers \(0^3 = 0, 1^3 = 1, 2^3 = 8, 3^3 = 27\)… are called cubes.

There is no straightforward geometrical representation of higher powers.